vol.7
宇宙進化の高精度シミュレーションで
ニュートリノの質量の大きさを探る

2021年7月、スーパーコンピュータ「富岳」のほぼ全ノードを用いて、「6次元ブラソフシミュレーション」と呼ばれる計算が行われました。この手法は、世界で吉川さんだけがコード開発に成功したものです。吉川さんはこの計算で、宇宙のごく初期から現在までのニュートリノの分布の変化を、従来よりもずっと精密に描き出すことに成功しました。ここに至るまでにはどのような道のりがあったのでしょうか?また、今回の結果はどのような科学的意義をもつのでしょうか?

宇宙大規模構造の形成に
影響を与えるニュートリノ
宇宙には数え切れないほどの数の銀河がありますが、その分布は一様ではなく、たくさんの泡がくっつきあったような構造をとっています。泡の膜にあたる部分に銀河が集まっており、泡の中にあたる部分にはほとんどありません。このような構造を「宇宙大規模構造」と呼びます。宇宙のごく初期にはほぼ一様に物質が分布していたのですが、わずかに密度の揺らぎがありました。そのため、密度の高い部分が重力で周囲の物質を引き寄せ、それがまた周囲の物質を引き寄せるということが繰り返され、粗密の差が次第に大きくなって現在の宇宙大規模構造が形成されたと考えられています。
このような宇宙進化の主役となったのはダークマターです。ダークマターは私たちの目には見えない正体不明の物質で、周囲に重力を及ぼすということしか分かっていません。しかし、「宇宙の質量の大半を占めており、銀河の分布に沿って分布している」と考えられています。そこで、ダークマターの分布の時間発展(時間が経つにつれてどう変化するか)をシミュレーションすることで、宇宙大規模構造の形成過程を探る研究が行われてきました。この計算には、ダークマターを多数の粒子で表し、その粒子が互いに重力を及ぼしながら運動すると見なす「N体シミュレーション」という手法が使われます。
さらに、2000年頃にニュートリノが質量をもつことが確実となり、宇宙進化のシミュレーションにニュートリノも採り入れようという動きが出てきました。「ニュートリノはとても軽いのですが、宇宙にはたくさんあって高速で飛び回っており、ダークマターが重力によって塊をつくるのを弱める効果があるのです。このため、ニュートリノについてもN体シミュレーションが行われるようになりましたが、精度は不十分でした」と、吉川さんは今回の研究の背景を語ります。
解けないのが常識だった方程式に挑戦
そこで、吉川さんは「ブラソフ方程式」を数値的に解く「ブラソフシミュレーション」という手法を使うことにしました。N体シミュレーションとの違いを説明しましょう。
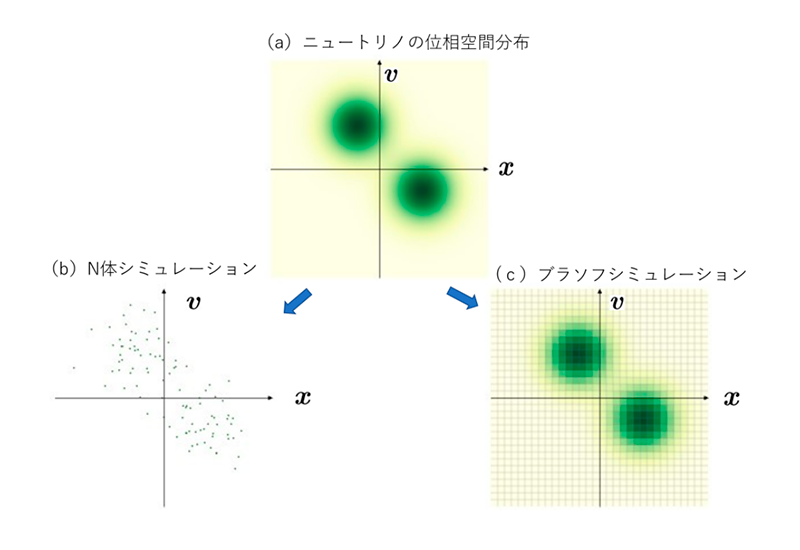
宇宙ではニュートリノがさまざまな位置にあり、さまざまな速度で動いています。これらのニュートリノを、位置と速度を座標とする仮想空間(位相空間という。位置も速度も実空間では3次元で表されるので位相空間は6次元となる)に置いて計算する(図1a)という点は、N体シミュレーションも、ブラソフシミュレーションも同じです。違うのは、N体シミュレーションではニュートリノ密度が高いところに「粒子」を置いてその位置と速度の時間による変化を計算する(図1b)のに対し、ブラソフシミュレーションでは位相空間を細かいメッシュに切り、その中でのニュートリノの分布の時間発展を計算する(図1c)ことです。実際のニュートリノは滑らかに分布している(図1a)ため、飛び飛びの粒子で表すN体シミュレーションでは大きなノイズが入ってしまいますが、ブラソフシミュレーションなら、密度の低いところもきちんと計算できるので精密なシミュレーションが可能になります。
図1
宇宙におけるニュートリノのN体シミュレーションとブラソフシミュレーション
宇宙の進化のシミュレーションでは、位置と速度を座標とする仮想空間(位相空間)に物質を置き、その運動を計算する。ニュートリノは位相空間において滑らかな分布をとっている(a)が、N体シミュレーション(b)では飛び飛びの粒子に置き換える。ブラソフシミュレーション(c)では、粒子を分布関数で表し、細かいメッシュを使うことによって滑らかな分布を再現できる。このため、N体シミュレーションよりもノイズが少なく、精密な計算結果が得られる。
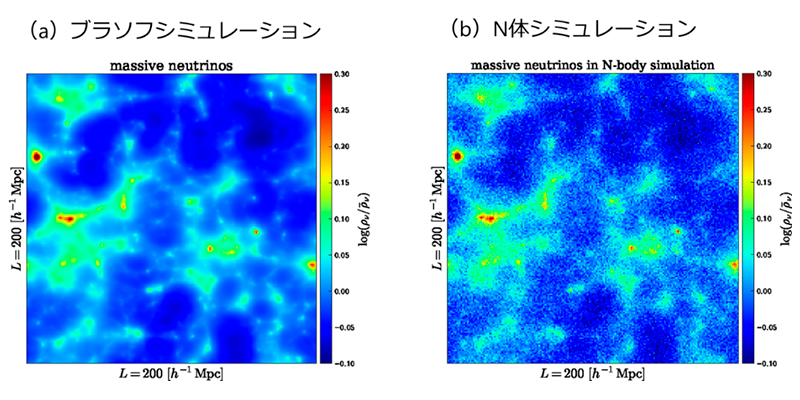
実際に吉川さんが計算した結果(図2)を見ると、ブラソフシミュレーションでは、ニュートリノの分布を滑らかに再現できていることが分かります。しかし、6次元ブラソフ方程式を解くには膨⼤な記憶容量と非常に高い計算性能をもつスパコンが必要な上に、計算量を抑えつつ精度の高い計算を行うためのアルゴリズムを開発する必要があるため、「解けるわけがない」というのが、研究者の間では長らく常識でした。吉川さんはその常識を覆したのです。
図2
ブラソフシミュレーションとN体シミュレーションの比較
ほぼ同じ規模のブラソフシミュレーション(a)とN体シミュレーション(b)とで求めたニュートリノの分布の例。ブラソフシミュレーションでは分布は滑らかであるのに対し、N体シミュレーションでは分布が粗く、細かい構造が埋もれてしまっている。
吉川さんがコード開発に着手したのは筑波大学に赴任した2007年。試行錯誤を重ねた末、2013年にT2K-Tsukubaという同大学のスパコンを使って、6次元のブラソフ方程式を解けることを実証しました。世界初の快挙でした。続いて、吉川さんは開発したシミュレーションコードで宇宙のニュートリノの分布という具体的な問題に取り組むことにしました。このテーマ選択には、東京大学の吉田直紀さんの助言もありました。
しかし、膨張する宇宙の中で6次元のブラソフ方程式を解くための数値計算法の開発はとても難しく、なかなか計算の精度が上がりませんでした。「何度もやめようと思いました」という吉川さんを救ったのは、海洋開発研究機構の簑島敬さんが提案した方法でした。二人はすぐに共同研究を始め、2017年には精度の高い計算ができるようになりました。その後、吉川さんはスーパーコンピュータ「京」など、さまざまなスパコンで計算を重ね、2019年の秋に、より高い精度を目指して、「富岳」共用前評価環境での実行を認められた課題として「富岳」での計算を開始したのです。
「富岳」の性能を引き出した全ノード計算
「富岳」は膨大なメモリを備えており、ノード間のネットワークが高速であり、高い並列化効率を達成できるので、多数のメッシュを並列計算するブラソフシミュレーションにはうってつけです。ただし、「富岳」はそれまでのスパコンとは異なるSIMD※1命令を採用しているため、計算を高速化するには「富岳」のSIMD命令に合わせてプログラムを書き換える必要がありました。吉川さんが高速化のためのアイデアを考案し、博士研究員の田中賢さん(現 京都⼤学基礎物理学研究所特定研究員)がそれをプログラムに実装することで、計算は一気に加速しました。
こうして2021年7月、「富岳」の全ノード(15万8976 ノード)の約93%にあたる14万7456 ノードを⽤いて、約400 兆個のメッシュを使ったニュートリノのブラソフシミュレーションが成功しました(図3a)。もちろん計算の規模は世界最大級で、過去に中国のスパコンで行われた同等規模のN体シミュレーションの10倍のスピードでした。
図3
「富岳」の14万7456ノードを用いたシミュレーションの結果
ニュートリノの分布の時間発展はブラソフシミュレーションで計算し(a)、ダークマターの分布の時間発展はN体シミュレーションで計算した(b)。いずれも実際の観測で得られた宇宙のごく初期(誕生から2億年程度)の物質の分布を初期値とし、現在(誕生から138億年)までの変化を計算した結果。ブラソフシミュレーションの時間ステップは、1ステップが約200万年。計算した宇宙空間は、1辺が1200 h-1Mpc(h-1Mpc は⻑さの単位。hはハッブル定数[Mpc]を 100 km/s/Mpc で規格化した変数で約0.7、Mpcはメガパーセク。1 h-1Mpcは約466万光年)の立方体で、観測できる宇宙をほぼカバーする大きさ。
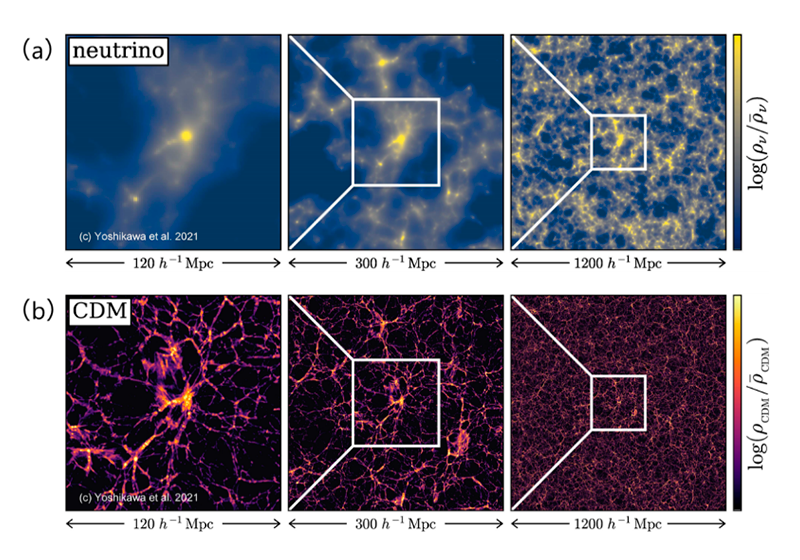
吉川さんは、ニュートリノをブラソフシミュレーションで扱いつつ、ニュートリノと相互作用するダークマターの分布はN体シミュレーションで時間発展させています(図3b)。「ニュートリノとダークマターのシミュレーション結果をつき合わせて解析し、実際の観測データと比べることで、まだ分かっていないニュートリノの質量の範囲を絞り込むことができます。地上での実験では求めることが難しいニュートリノの質量が、宇宙の観測とシミュレーションから分かる可能性があるのです」と吉川さんは今回のシミュレーションの科学的な意義を説明します。当然ながら、ニュートリノの質量が分かれば、ニュートリノが宇宙大規模構造の形成に与えた影響も明らかになります。さらに、ブラソフシミュレーションは、ブラックホールに物質が吸い込まれていくときにできる「降着円盤」や太陽系の惑星間空間における磁気嵐など、宇宙で起こるさまざまな現象に関係する磁気プラズマの研究にも活躍すると期待されています。
吉川さんは、「今回の計算は、実質的に「富岳」の全ノードを使っただけでなく、各ノードのメモリも使い切るようなぎりぎりの計算でした。ハード面でもソフト面でもいろいろなトラブルがありましたが、それを乗り越えて計算を最後まで達成した経験は、今後の「富岳」の運用にフィードバックされ、「富岳」の性能を引き出すのに役立っていくと思います」と振り返ります。今回の実質的全ノード計算は、「富岳」の活用に弾みをつける大きな推進力となることでしょう。
研究者紹介

自分の好きなことをやって生きていけるから研究者になろう――吉川さんは中学生のときからずっとそう思っていたそうです。1995年、大学3年生のときに、当時はまだ一般的ではなかった数値シミュレーションができることにひかれて宇宙物理学の教室に入りました。そこでブラソフ方程式に出会い、「いつか自分の手で解こう」と決意したのです。「誰もやっていないことをやる」という研究姿勢は、学生にも教えています。鈴鹿市出身ということもあり、趣味はモータースポーツ観戦。「ひたすらスピードを追求するところが分かりやすくていい」とのことです。
研究課題名:
宇宙の構造形成と進化から惑星表層環境変動までの統⼀的描像の構築(hp200124/ hp210164)
課題代表者:神戸大学 牧野 淳一郎
(2021 ACMゴードン・ベル賞ファイナリスト研究成果)
趣味とチャレンジ精神で編む人生

私は今でこそ理研計算科学研究センターの技師として「富岳」を用いた研究開発に携わっていますが、子供の頃は他の子よりちょっとコンピュータをいじるのが好きだっただけで、まさかスーパーコンピュータ開発の最前線に関わる人生になるとは夢にも思っていませんでした。
初めてプログラミングらしいことを始めたのは中学生の頃です。簡単なゲームを作ろうとして挫折したことだけは覚えていますが、何度も手を出しては上手くいかずに投げ出していました。その後プログラミングは忘れ、大学に進学してからは一転、スクーバダイビングを始めます。元々小さい頃から海や山といった自然が好きで、非常に綺麗な海中写真に惹かれたのがきっかけです。そうして海洋や気象といった地球科学に強く興味を持ち、生物系や化学系に進む人が多い環境科学科という学科の中では珍しく、地球科学系へと進みました。
理研と関わりを持ったのは博士3年。気象学を専攻して論文を書きつつ研究職の当てを探していた時に、当時の複合系気候科学研究チームで計算サーバ・ストレージ管理のアルバイトとして雇われたのが最初です。計算科学のイロハも知らず、趣味で細々とやっていたサーバ管理スキルを買われたのがきっかけでしたが、その後も気象学と計算科学の両面でポスドク、研究員として雇われ、今の技師になるまでやってこられました。
現在は技師の仕事の傍ら、「富岳」の性能を活かし、計算コストに対して計算速度・精度ともにバランスの取れた結果を出せる気象モデルの枠組みを念頭にした研究開発も行っています。子供の頃の2つの趣味が融合した形で今の仕事に携わることができ、本当に運が良かったと思いますが、二足の草鞋と笑われないよう、これからも精進していきたいと思います。
次回は、「富岳」を用いて全球雲解像モデルNICAMの開発に携わる、海洋研究開発機構 環境変動予測研究センター 雲解像モデル開発応用グループに所属する新進気鋭の若手、高須賀大輔ポストドクトラル研究員につなぎます。

大学時代、鹿児島県喜界島にてダイビング部の夏合宿に参加した折に撮影した海中風景写真。

